Kakuro, or Cross Sums, are more like traditional math games than Sudoku.



WELCOME TO PUZZLES-ONLINE-NICHE


Traditional math games require addition and subtraction operations as a bare minimum, that is

why we feel that Kakuro ( or Cross Sums), though not quite as popular, are certainly more like

traditional math games than Sudoku.

KAKURO/KAKKURO

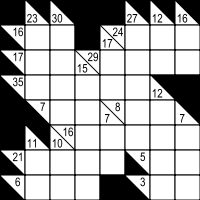
Comes from the Japanese expression for 'cross addition' ( kasan kurosu, (加算クロス), or simply abbreviated, KA-KURO. Like it's cousin Sudoku, Kakuro uses a grid ( though typically 16 x 16), other grid sizes are also possible. The clues in Kakuro math games consist of numbers, arranged in the grid , as shown to the right.

The object is to solve the 'clues', using only the numbers 1-9, one number per cell, such that the sum of the numbers in each entry match the associated clues, and that no digit is repeated in any single entry.


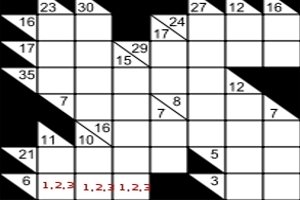
As an example , the clue in the bottom left corner is 6, by Kakuro rules, we need to enter the sum , using only the numbers 1-9, with no number repeated in the entry.

The only possible combination would be 1,2,3 in some order, we have entered the possibles in the diagram to the right.


To further solve this puzzle we need to investigate the possible combinations in other blocks.


In an adjacent block we have the clue '11', in two , which means we need to sum two numbers from 1-9 which equal 11. The only possibilities are 2 +9, and 3+8, therefore we can eliminate '1' from the first block, and our grid might now appear as follows:


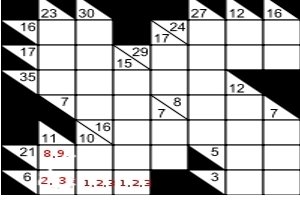HELPS/HINTS/STRATEGIES

  • CLUES:

Remember the 'clues' , which are the numbers in triangular boxes

in the the grid, are referred to by their number and then the number of

cells included to solve it. So we would call the clue in the top left corner

( in our diagrams above) "23" in-three.

(Three referring to the number of cells ( or numbers needed to solve the clue)).


A clue such as "45", uses 9-cells, because the sum of the numbers 1 through

9 = 45, therefore it is implied and unecessary to write "45 in nine".


  • PATTERNS :

Having played Kakuro for more than 30 years , I can tell you their are certain

patterns, or clues which have the same answers , no matter what.

Learning or understanding such patterns is vital in solving Kakuro puzzles.

Here are the patterns

24-in-three: Always contains the numbers {9,8,7}, in some order

23-in-three : Likewise always has the same members { 9,8,6}.

17-in-two: {9, 8} some order.

16-in-two: {9, 7} some order.


  • STRATEGIES:

Armed with the above patterns, we can now develop some solid Kakuro

puzzle solving strategies.

CROSSING TECHNIQUE:






Kakuro Variants/Resources:






From Math Games Kakuro to Math Puzzles

From Math Games Kakuro to Puzzle Games Online