We have some of the absolutely best Free LOGIC PUZZLES on the web!
- FREE LOGIC PUZZLES
Included in our logic puzzle selections below you will find syllogisms, grid logic, grid-less logic and a special bonus section for an interactive puzzle challenger called Halma( You can go directly to those pages by clicking the links ) , or read on for some interesting background information about the origins of logic puzzles and a discussion of deductive reasoning , on this page.
NEWS FOR DECEMBER :
***** HOT OFF THE PRESSES*****
WE ARE PLEASED TO ANNOUNCE OUR FIRST E-BOOK , A COMPILATION OF 'OUR BEST LOGIC PUZZLES' JAM-PACKED WITH OVER 80 LOGIC PUZZLES FROM OUR WEB-PAGES.
OUR BEST LOGIC PUZZLES (COMPILATION)
PICK UP THE E-BOOK VERSION HERE FOR ONLY $4.99.
OR YOU CAN OBTAIN THE PAPER-BACK COPY :
HERE FOR $8.99 OR AT AMAZON.COM
CONTENTSFree Logic Grid Puzzles(For KIDS) |
NEWS/UPDATESWE have just added a new and exciting update to our Grid Logic pages : INTERACTIVE GRID LOGIC is here ! : |
LOGIC
So what is Logic?
Logic is a system of reasoning, it is the art of applying reasoning to the structure and content, the method of deduction.
In my humble opinion the grandfather of the modern puzzle would have to be none other than Charles Lutwidge Dodgson, ( who you might know better as Lewis Carroll , author of 'Alice In Wonderland ' ). In his book 'The Game of Logic' Carroll introduced a game to solve problems such as confirming the conclusion "Some greyhounds are not fat" from the statements "No fat creatures run well" and "Some greyhounds run well".
( Puzzles like this, where we are given a list of premises and asked what can be deduced from them, are known as syllogisms ).
Click this link to get started with : Free Printable Syllogisms , or read on to discover more about deductive reasoning.
DEDUCTIVE REASONING
One of the main principles of logic is Deductive Reasoning (reasoning from the general to the particular). It involves using given true premises to reach a conclusion that is also true. If the rules of deduction are followed, this ensures we reach an accurate conclusion.
|
An Example: 1. All people named Sally sell sea shells at the sea shore. (general) 2. My Friend's name is Sally. (particular) 3. Therefore, Sally sells shells at the sea shore. - (A conclusion from deducing the premises of the first 2 statements). |
Or, as an additional example consider : 1. All men are mortal. (general), 2. I am a man. (particular), 3. Therefore, I am mortal. ( DEDUCTION ) |
Both examples above use deduction , and these types of problems are syllogisms (again where one takes two separate conditional statements, and deduces a logical conclusion by combining the hypothesis of one statement with the conclusion of another).
To summarize , we might generalize a logical deduction as follows:
1. If , P -- > Q .
2. Q -- > R .
3 Then P -- > R .
Click this link to get started : Free Printable Syllogisms , or read on for our discussion on 'Logic Grid Puzzles' below.
LOGIC PUZZLES:GRIDS
|
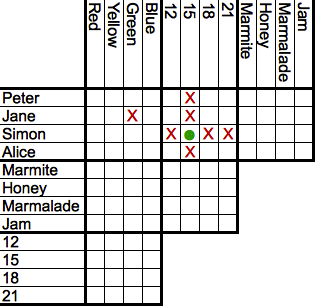
Another form of logic puzzle, popular among puzzle enthusiasts and available in magazines dedicated to the subject, is a format in which the set-up to a scenario is given, as well as the object (for example, determine who brought what pet at a pet store , and on what day each pet was bought), some specific clues are given ("neither Mary nor Ray purchased the German Shepherd"), and then the reader fills out a matrix with the clues and attempts to deduce the solution. Common logic puzzle magazines are derivatives of the logic grid puzzle called "table puzzles" that are deduced in the same manner , but lack the grid either because a grid would be too large, or because some other visual aid is provided. For example, a map of a town might be present in lieu of a grid in a puzzle about the location of different shops. |
 |
Click here for some additional fun with free Logic Grid Puzzles , or try these ( 'Table Puzzles') , which we will refer to here as Logic Grid-Less Puzzles
We are pleased to announce the addition of an 'old' new logic grid puzzle called Halma.
Check it out here: HALMA INTERACTIVE PUZZLE LINK
ADDITIONAL RESOURCES/LINKS
Riddles:
If you try to fail and succeed, what have you done?
Does 'expect the unexpected' make the unexpected expected?
If we are here to help others, what are the others here for?
If corn oil is made from corn and olive oil made from olives, what is baby oil made from?
More Riddles:
If you have a bunch of odds and ends and throw away all but one, what do you have left?
Would a fly without wings be called a walk?
Why is 'abbreviation ' such a long word?
What was the best thing 'before' sliced bread?
Why isn't there mouse-flavored cat food?
Why is the person who invests your money called a broker?
The Social network based search engine & news service
Who links to my website?